
The fundamentals lesson provides a summary overview of basic math skills required on the SHSAT. Material includes fundamentals learned prior to Algebra. For further in-depth lessons on any one skill, please advance to the SHSAT Math Toolbox.
Khan Academy (Basics Plus)
Math Is Fun (Basics Plus)
Part 1 begins on the Introduction lesson page.
The Story of Eratosthenes – Critical Thinking Adventure Part 2
Back in the world of ancient Egypt around 245B.C., in the absence of what we take for granted as modern technology, Eratosthenes had an idea. He knew the observations at the well and the lack of shadows from columns at Syene were the result of the earth’s tilt (currently 23.4°, but that oscillates between 22.1º and 24.5º). The city of Syene at 24° north was almost precisely on the line of the Tropic of Cancer shown in the diagram below. As a result, at noon on June 21, the highest point of the sun in the sky, the sun was neither to the north nor to the south in the sky, but directly overhead from Syene. Of course there was no such thing as the Tropic of Cancer in 245B.C. or even the concept of lines of latitude and longitude. How do we know? Because Eratosthenes was the first to create such lines and attempt to map the known world based on them.
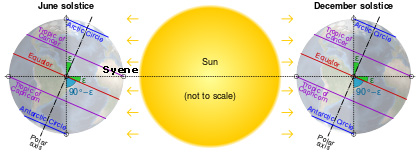
Eratosthenes also knew the observations from Alexandria, nearly 500 miles away where the sun was not directly overhead at noon on June 21, were the result of the curvature of the earth. A straight column or stick protruding vertically from the surface at Alexandria would not be parallel to the sun’s incoming rays if the earth were curved. They would cast a measurable shadow.
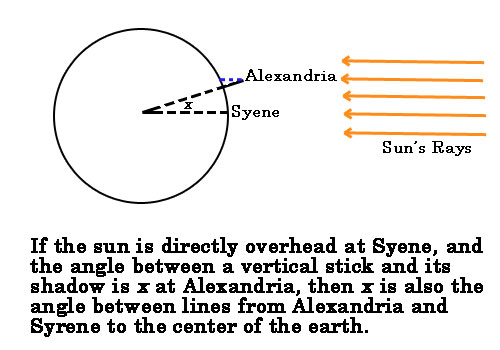
The measure of the shadow relative to the size of the vertical stick or column determined the angle, x, of a right triangle formed between the vertical stick and the horizontal shadow along the earth’s surface. Furthermore, the difference in angles of the shadows between both locations was only the angle of the shadow at Alexandria by design because the angle of the shadow at Syene was zero. Thus Eratosthenes only had to make one measurement to find the angular difference, x. Furthermore, Eratosthenes knew that the difference in angles, x, produced by the shadows at both locations was the same as the angle from the center of the earth to the surface at both locations. Thus, if he knew the distance between Alexandria and Syene he could use the angle to figure out what fraction of the full distance around the globe that distance from Alexandria to Syene represented. In other words, in reverse order Eratosthenes could calculate the distance around the globe given the known distance from Alexandria to Syene. Of course, Eratosthenes did not have the benefit of circular trigonometry nor did the measurement of degrees exist at the time so he did not know the angle x was 7°14′ or at least he did not express it that way. Nevertheless, Eratosthenes could measure the shadow length versus the column and assess the angle formed in the right triangle was a fraction, 1/50, of a complete rotation. Eratosthenes concluded the nearly 5,000 stadia distance (approximately 800 km by our current measurements) between the two cities represented 1/50 the distance around the globe. That equated to 252,000 stadia or 40,000km around the globe. Current measurements put the circumference of the earth around 40,075km at the equator. Remarkable!
Of course the accomplishment was not so remarkable for the accuracy of the result as it was for the methodology. One key to Eratosthenes’ result is the fact that the angle formed by the shadow at Alexandria equals the angle formed by lines from the center of the earth to the two cities on earth’s surface. Without that connection Eratosthenes could never calculate the distance around the earth. Can you explain with one theory learned in the upcoming chapter why those two angles are equal?
Part 3 begins on the Algebra-Word Problem Fundamentals page.
